이미지 인식 분야에서 사람을 능가하는 성능을 보여주는 딥러닝 모델인 CNN을 시계열 데이터에도 적용하기 위해 다양한 시도와 접근들이 이뤄지고 있었고 가장 직관적으로 생각할 수 있는 접근 방법으로는 시계열 데이터를 이미지로 표현하는 것이었습니다.
하지만 시계열 데이터를 이미지로 표현하는 것은 정보손실이라는 문제로 이미지로 바꾸는 것은 쉽지 않은 일이였고, Recurrence Plot 이라는 알고리즘을 통해 시계열 데이터를 이미지로 변환하는데 성공을 하였습니다.
시계열 데이터를 이미지로 바꾸게 될 경우 장점은 일단 CNN구조로 이루어진 다양한 알고리즘의 모델들을 시계열 데이터에도 적용이 가능해진다는 점입니다. 그점 땜에 유용하게 사용이 가능할 것으로 판단 됩니다.
RP(Recurrence Plot)는 시계열 데이터를 이미지화 시킬경우 아래와 같은 결과가 나오게 됩니다.

밑에 내용은 이론적인 부분으로 RP가 동작하는 방식에 대해 자세히 나와있습니다. 밑의 이론은 아래의 블로그의 내용을 그대로 인용해서 가지고 왔습니다.
blog.naver.com/rkdwnsdud555/221380407792
CNN모델에 시계열 데이터를 사용하기 위한 이미지 표현화
CNN모델에 시계열 데이터를 사용하기 위한 이미지 표현화 이미지 인식 분야에서 매우 좋은 성능을 보이...
blog.naver.com
시계열 데이터를 RP를 이용해 이미지로 변환하는 과정
Step1. 시계열 데이터의 m차원 공간 궤적 구성
Step2. m차원 공간 궤적을 RP행렬로 표현
우선 일반적으로 시계열 데이터를 시간의 흐름에 따라 표현한 경우에는 아래의 이미지와 같습니다.
x축은 시간을 나타내며, y축은 해당 시간의 측정값이 됩니다.

이미지 출처 : https://arxiv.org/pdf/1710.00886.pdf
이를 데이터로 표현한다면,
a) [0, 1, 2, 1, 2, 3, 4, 3, 2, 3, 2, 1]
b) (1,0), (2, 1), (3,2), (4,1), (5,2), (6,3), (7,4), (8,3), (9,2), (10,3), (11,2), (12,1)
등으로 나타낼 수 있습니다.
Step 1.에서는 시계열 데이터의 m차원 공간 궤적을 구합니다. 아래의 이미지는 m이 2인 경우입니다.
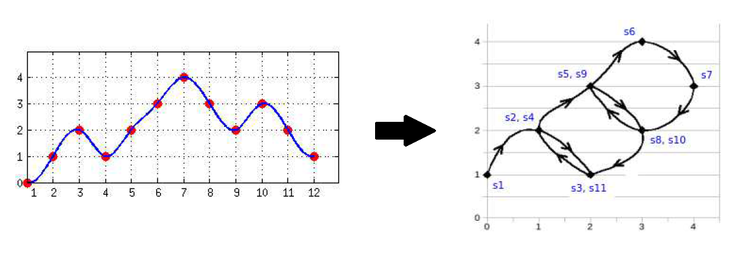
이미지 출처 : https://arxiv.org/pdf/1710.00886.pdf
m이 2인 경우 시계열 데이터의 2차원 공간 궤적은
s1: (x1, x2) s2: (x2, x3), s3: (x3, x4), ... , sn : (xn, x(n+1)) 로 계산할 수 있습니다.
좀 더 쉬운 이해를 위해 구체적이 예를 들어보겠습니다.
이미지의 좌측 시계열 데이터는 다음과 같습니다.
[x1: 0, x2: 1, x3: 2, x4: 1, x5: 2, x6: 3, x7: 4, x8: 3, x9: 2, x10: 3, x11: 2, x12: 1]
이를 2차원 공간 궤적으로 표현할 경우
s1: (0, 1), s2: (1, 2), s3: (2, 1) ..., s11: (2, 1) 로 변환됩니다.
s1 = (x1, x2) | x1은 0 이고 x2는 1 이므로 s1 = (0, 1)
s2 = (x2, x3) | x2는 1 이고 x3은 2 이므로 s2 = (1, 2)
이해 되시나요?
s1은 x1에서 x2로의 궤적을 의미합니다.

s2는 x2에서 x3로의 궤적을 의미합니다.

따라서, 일반화를 하면 Sn은 Xn -> X(n+1)의 궤적이라고 볼 수 있습니다.
이 과정에서 m은 2보다 클 수 있으며 시간축의 움직임은 한 칸보다 클 수 있습니다.
step 2. 에서는 앞에서 구한 시계열의 m차원 궤적을 이용해서 거리 행렬을 구합니다.

이미지 출처 : https://arxiv.org/pdf/1710.00886.pdf
우측의 이미지를 행렬 R이라 할 때, Ri,j 는 다음과 같습니다.
[Cross recurrence plots]

e(엡실론) : 거리 역치값
θ(x) : 단위 계단 함수 (Heaviside step function)
쉽게 말해, Ri,j는 Si 와 Sj의 거리입니다. 다만 거리에 약간의 최소기준치(e)와 반올림을 취했을 뿐입니다.
그냥, 두 s간의 거리를 행렬로 표시했다고 생각하셔도 무관합니다.
예를 들어, 행렬 R의 (1,1)의 값은 s1(0,1) 과 s1 의 거리입니다. 당연히 0이 됩니다.
R(1,2)의 경우 s1(0,1)과 s2(1,2)의 거리입니다.
단순하게 직선거리로 계산한다면

가 됩니다.
이런 식으로 모든 조합의 s간 거리를 기록한 것을 RP 행렬이라 부르며, 이는 이미지로써 사용할 수 있습니다.
정리하자면, RP알고리즘은 시계열 데이터에서 m차원의 움직임 궤도간의 거리를 2차원 행렬로 표현하는 방법이라고 볼 수 있습니다.
아직 이해가 안되신 분들을 위해 보다 단순한 Recurrence Plot 표현법을 살펴보겠습니다.
[Recurrence plot]

인 경우 이미지는 1과 0 값으로만 표현됩니다.

이미지 출처 : https://en.wikipedia.org/wiki/Recurrence_plot
Recurrence Plot의 의미
Recurrence Plot에 의해 변환된 시계열 이미지의 각 점이 의미하는 것이 무엇일까요?

식에서 확인 할 수 있듯 점이 찍히기 위해서는 두 궤적의 거리가 e보다 작아야 합니다. 따라서 RP 행렬은 궤도가 같은 위치에 있는 시간 쌍의 모음을 묘사합니다.
이러한 표현을 통해 우리는 많은 정보를 얻을 수 있습니다.
예를 들어, 궤도가 주기 T를 통해 엄격하게 주기적이면 모든 시간 쌍은 T의 배수로 분리되어 대각선으로 표시됩니다.

RP의 시각적 표현은 시계열 데이터의 역동성에 대한 힌트를 제공합니다.
보다 자세한 RP에 대한 설명은 Recurrence Plots of Dynamical Systems에서 확인할 수 있습니다.
자, 이제 시계열 데이터를 이미지로 표현하였으니 CNN모델을 이용하여 다양한 이미지 처리를 수행할 수 있게되었습니다.
Classification of Time-Series Images Using Deep Convolutional Neural Networks 연구에서는 RP를 이용하여 시계열 데이터를 이미지로 표현한 후 아래와 같은 구조의 CNN을 적용하여 UCR 시계열 데이터를 분류 하였습니다.

이미지 출처 : https://arxiv.org/pdf/1710.00886.pdf
UCR 시계열 데이터 분류 결과

이미지 출처 : https://arxiv.org/pdf/1710.00886.pdf
동일한 데이터 세트에 대해 기존 혹은 최신 시계열 데이터 알고리즘과 비교하였을 때, 대부분의 데이터 세트에서 오차율(잘못 분류된 데이터의 비율)이 많이 개선된 것을 확인할 수 있습니다.
따라서, RP를 이용해 시계열데이터를 이미지로 표현했을 경우 해당 이미지가 시계열 데이터의 유의미한 정보를 충분히 포함하고 있다고 볼 수 있습니다.
[참고문헌]
1. Nima Hatami, Yann Gavet and Johan Debayle, Classification of Time-Series Images Using Deep Convolutional Neural Networks, 2017.
2. J.-P. ECKMANN, S. OLIFFSON KAMPHORST, D. RUELLE, Recurrence Plots of Dynamical Systems, 1987.
3. https://en.wikipedia.org/wiki/Recurrence_plot
이론적인 부분은 위에서 설명이 끝이났고, 이제 코드를 통해 간단히 구현이 가능합니다.
먼저 사용할 라이브러리들을 import 시켜줍니다.
import pandas as pd
import numpy as np
import pylab as plt
import matplotlib.pyplot as pplt
from scipy.spatial.distance import pdist, squareform라이브러리들이 import 되었으면 rec_plot이라는 함수를 선언하여 RP알고리즘을 설계합니다.
def rec_plot(s, eps=0.01, steps=10):
d = pdist(s[:,None])
d = np.floor(d/eps)
d[d>steps] = steps
Z = squareform(d)
return Z이제 main문을 작성을하시면 코드가 끝이나며 결과를 얻으실 수 있습니다.
df = pd.read_excel("TNT_many_TSC.csv")
#train = data_frame[['copy 0']]
df = df['TNT']
df = df[:2000]
df.plot(figsize=(16,4))plt.imshow(sub_s1)
plt.savefig('a.png')저의 경우는 csv파일에서 TNT라는 부분을 2000개의 셀만을 이용하였습니다.


위에와 같은 결과를 얻을 수 있고, 여러개의 결과를 eps라는 값을 변경해가면서 얻으실 수 있습니다.
eps값은 위의 이론에서 설명한 엡실론 값입니다.
df = pd.read_excel("TNT_many_TSC.csv")
#train = data_frame[['copy 0']]
df = df['TNT']
df = df[:2000]
df.plot(figsize=(16,4))
a = []
sub_s1 = rec_plot(df, eps=0.10)
sub_s2 = rec_plot(df, eps=0.30)
sub_s3 = rec_plot(df, eps=0.60)
sub_s4 = rec_plot(df, eps=0.80)
sub_s5 = rec_plot(df, eps=5)
a.append(sub_s1)
a.append(sub_s2)
a.append(sub_s3)
a.append(sub_s4)
a.append(sub_s5)
fig, axs = plt.subplots(1, len(a), figsize=(16, 4), sharey=True)
print(fig)
print(axs)
for i,obj in enumerate(a):
axs[i].imshow(obj, cmap='gray')
img = axs[i].imshow(obj)
plt.savefig('a.png')


'코딩 > python - 코드' 카테고리의 다른 글
| [python] Gramian Angular Field로 시계열 데이터 이미지화 (0) | 2021.11.25 |
|---|---|
| SciPy와 matplotlib를 이용한 시계열 데이터 피크 검출 (0) | 2021.07.09 |
| [python] file 소켓을 통한 txt파일 전송 서버->클라이언트 (0) | 2020.11.10 |